Two kinds of Prisms

If you are a functional programmer, you have probably heard of lenses and prisms. They are bidirectional structures often said to be dual to each other. You might know them from Haskell’s lens library, the recent paper on Profunctor Optics, or other places (such as my two blog posts (1, 2).

While lenses are extensively used in practice and a topic of considerable discussion, the same cannot be said for prisms: they seemingly hold a more mysterious flavour. What is even a prism? What does it do operationally, and what does it mean to be dual to a lens? In this blog post I unpack the answers to these questions, and show that there are two different but related ways of being dual to a lens, and that the way in which they are related is subtle, not obvious, and does not generalise to dependent types. This is not something I have seen discussed before, so I am recording it here for posterity.

Let’s just quickly recap what a lens is, and how it’s related to an optic. Given a cartesian category \(\mathcal{C}\), a lens \((A, A') \to (B, B')\) consists of the forward map \(\text{get} : A \to B\) and the backward map \(\text{put}: A \times B' \to A'\).¹ Lenses are morphisms in the category \(\mathbf{Lens}(\mathcal{C})\) whose objects are pairs of objects in \(\mathcal{C}\). This is their concrete definition. You can also see lenses as special cases of optics. An optic \((A, A') \to (B, B')\) over a monoidal category \(\mathcal{M}\) is defined as an element of the following coend \(\int^M \mathcal{M}(A, M \otimes B) \times \mathcal{M}(M \otimes B', A')\). If you set the monoidal category \(\mathcal{M}\) to be the previously defined cartesian category \(\mathcal{C}\), then you can reduce the above representation to lenses.²

Great, so how is a prism dual to a lens? There are two ways. Given a cocartesian category \(\mathcal{C}\), you can define a prism as either:

• an element of the hom-set \(\mathbf{Optic}(\mathcal{C})((A, A'), (B, B'))\), or
• an element of the hom-set \(\mathbf{Lens}(\mathcal{C}^{op})((A, A'), (B, B'))\).

The first definition is dual to a lens because we’re instantiating optics for a cocartesian (instead of a cartesian) category, and the second definition is dual because we’re instantiating lenses in the opposite category. Many people casually reference prisms as being dual to lenses, but they seldom reference which duality they’re referring to. And as it turns out that, while these are related, they give a markedly different way of thinking about prisms. Let’s see why.

If we unpack the prism-as-optic definition, we have the following chain of isomorphisms:

where the first isomorphism is given by the universal property of coproduct, and second one by Yoneda reduction. This gives us two types of maps in \(\mathcal{C}\) which we’ll call \(\text{match} : A \to A' + B\) and \(\text{build} : B' \to A'\). If we unpack lens-in-the-opposite-category definition, we get this chain:

The two resulting maps are also often called \(\text{build} : B \to A\) and \(\text{match} : A' \to A + B'\). Let’s write them both unpackings side by side.

It’s clear that they’re different! Even though they have the same “shape”, the way the ports \((A, A')\) and \((B, B')\) are bound to parts of the two maps are different in these two cases.

So what does this mean, and why is this important? Well, I’m trying to understand what prisms “really” do, in the operational sense. Where does information first enter? What happens to it? Is there branching or copying? Is some additional information required to produce certain kind of output? And so on. These are important for actually building something using prisms. But I only have a clear picture for one of the definitions. It’s the one that sees them as optics.

I wrote about this definition in my previous blog post. I also animated it below: we start at \(A\), and then we either a) short-circuit the computation by moving straight down back to \(A'\), or b) we query the environment with a \(B\) and wait for a response \(B'\), subsequently turning it into an \(A'\).

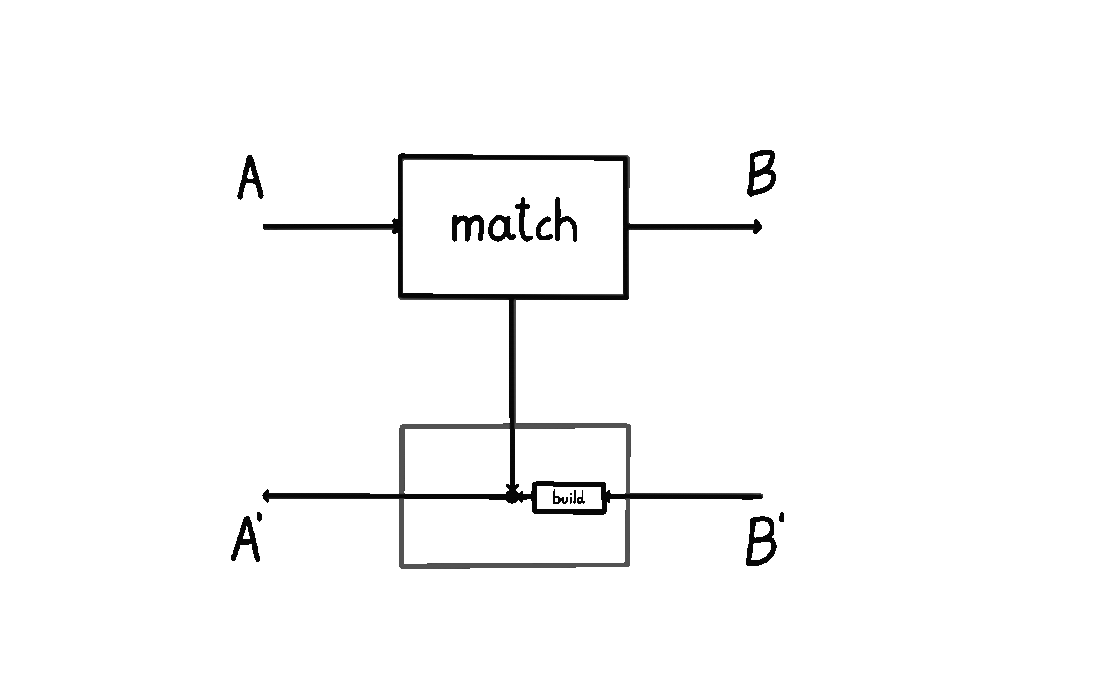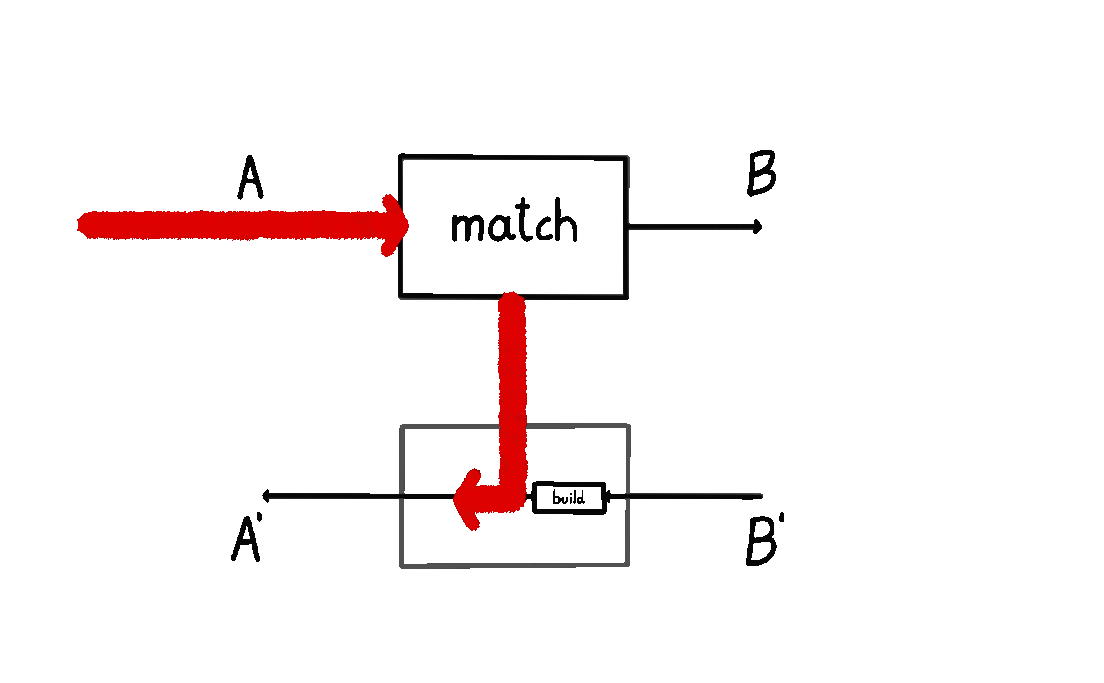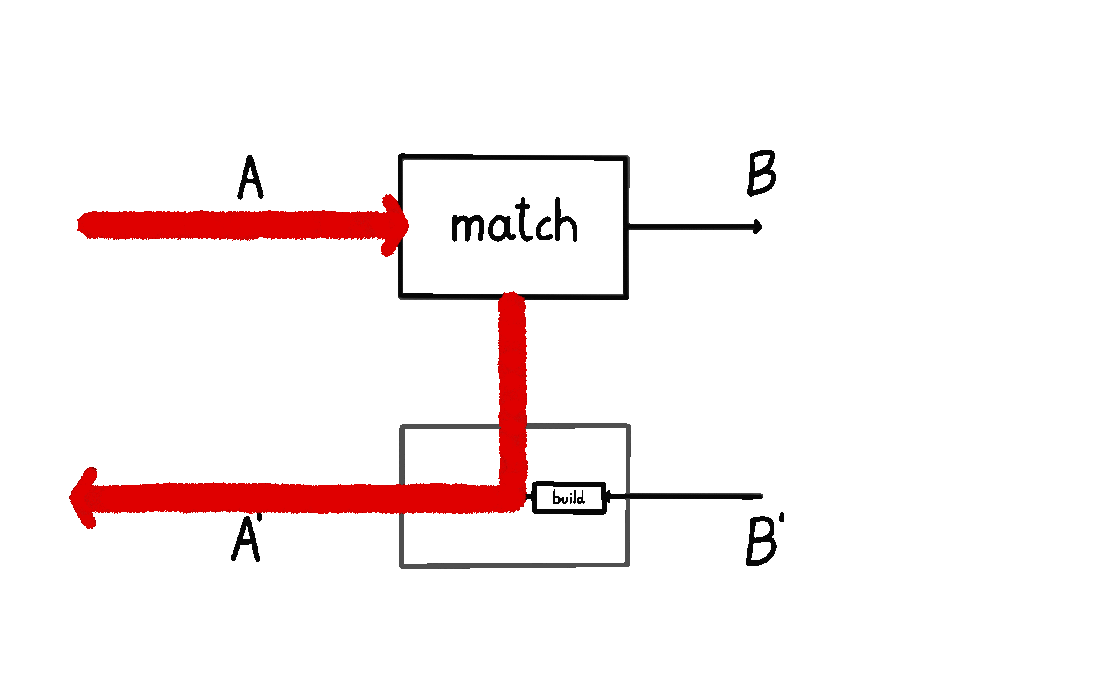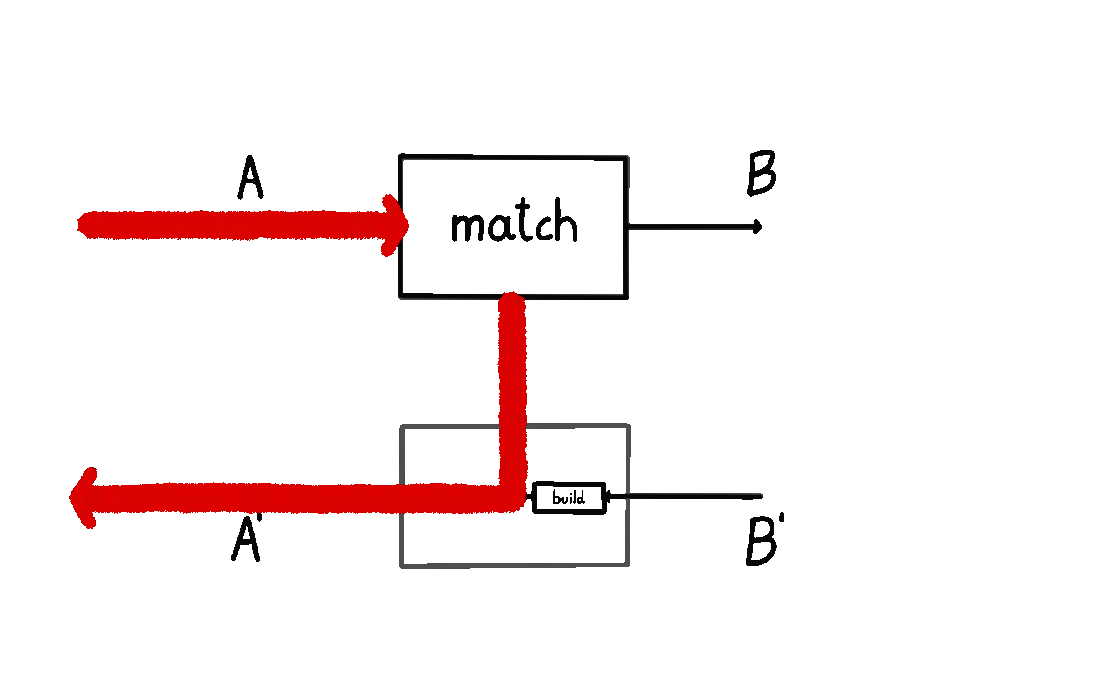
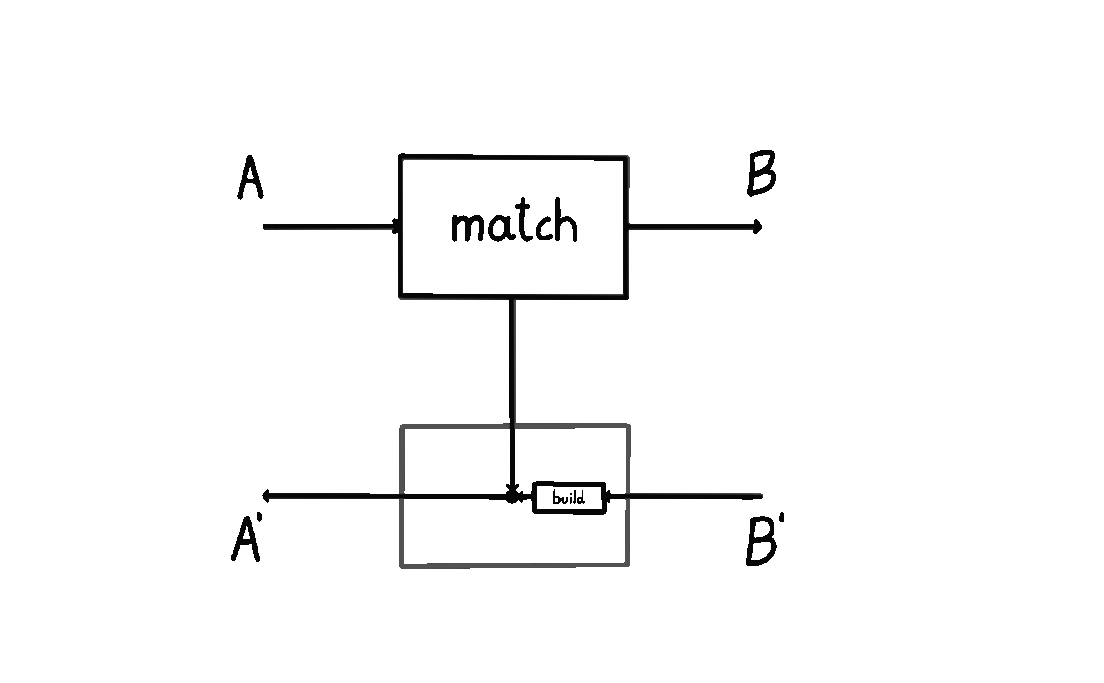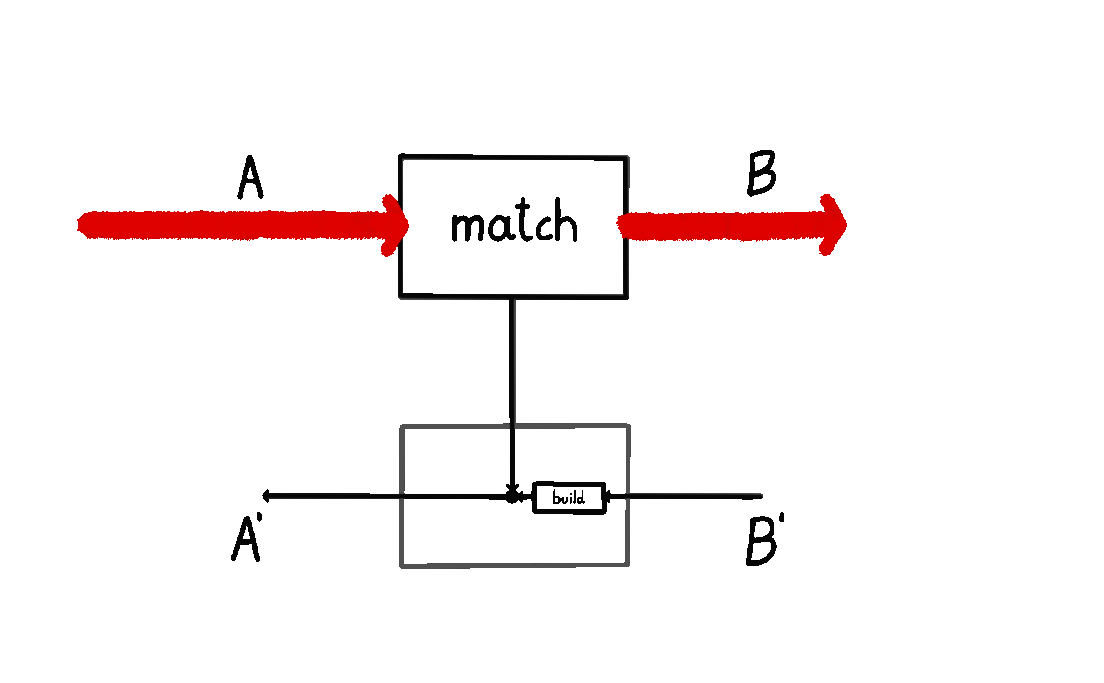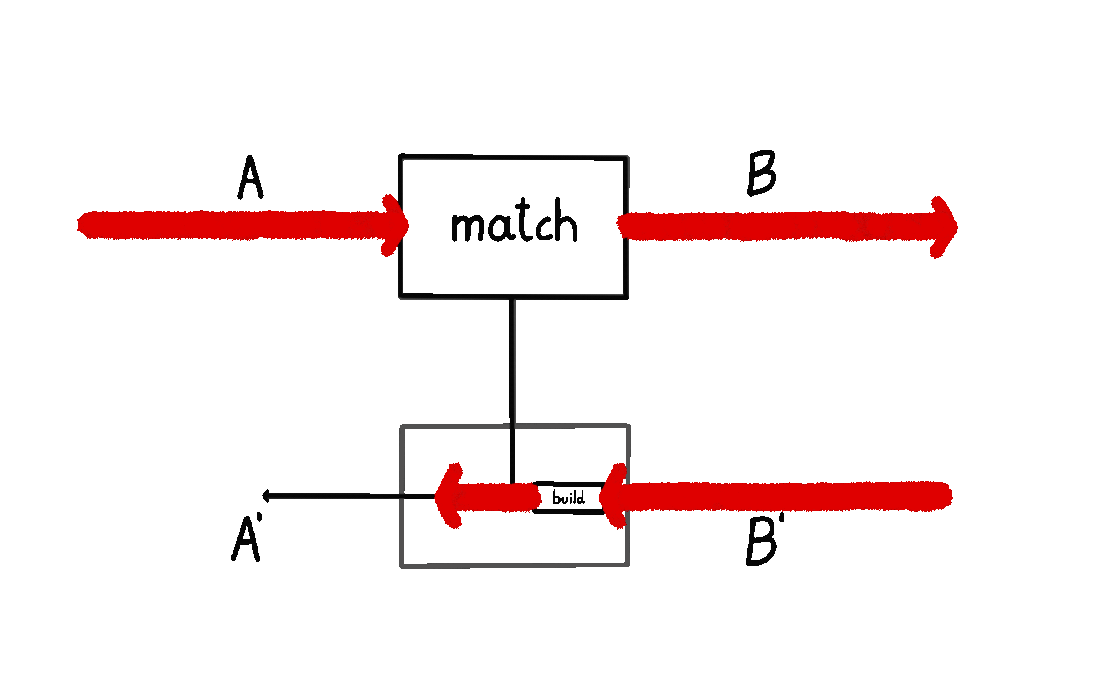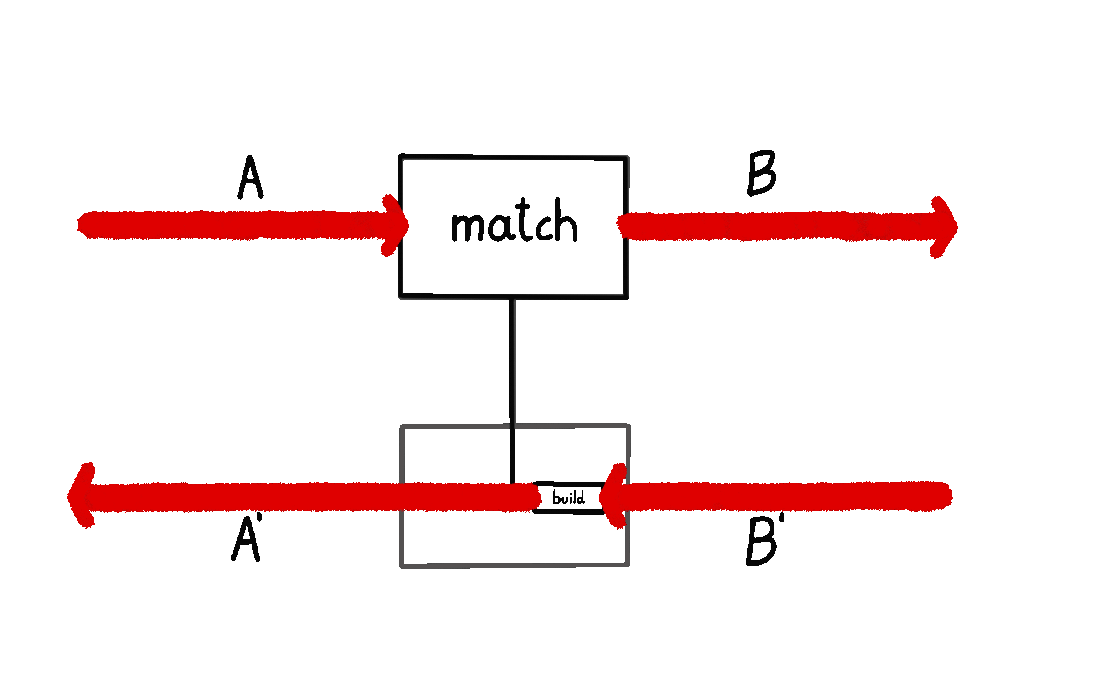
The other picture – where a prism \((A, A') \to (B, B')\) consists of maps \(\text{build} : B \to A\) and \(\text{match} : A' \to A + B'\) – does not give us anything like that. Which way does the information flow here? Does \(\text{build}\) happen before \(\text{match}\)? Do we start at \(B\), and then build an \(A\), meaning we go backwards? Or is there something else at play? It’s not clear. People usually say “prisms are lenses in the opposite category” and then stop there, without telling us how to think about the internal data flow.

As it turns out³, these two dualities are related by the following subtle isomorphism:

This isomorphism simply takes the opposite of category of optics, but the reason why it is subtle is because on objects it swaps the order of forwards and backwards morphisms! That is, given a pair \((A, A')\) on the left, we map it to \((A', A)\) on the right. On morphisms, it ends up doing the only thing it can! (It’s worth unpacking this for yourself) This then explains why we had two different dualities – this was because we had not applied the approrpiate swap of forwards and backwards objects.

While this is a well-defined isomorphism, it breaks when we move on to the dependent case, i.e. where the type of the backwards objects depends on the value of the forwards one. In this case we no longer have the luxury of swaps, and dependent prisms take on a whole new form. This is the main reason I prefer the optic definition of prisms. The other reason is that it provides us with a mechanism for composing prisms with lenses to obtain affine traversals. Such a mechanism is missing from the other definition.

This makes me skeptical about using the second definition in practice. I haven’t been able to find any nice stories about the other definition, and at this point, I’m starting to wonder whether the fact that “prisms are lenses in the opposite category” is just a misleading coincidence applicable only in the non-dependent case, and only when the only optics of interest are prisms themselves.