Towards Categorical Foundations of Learning

Having put up on Arxiv our paper on Categorical Foundations of Gradient-Based Learning, I thought I’d write a short post updating everyone on the progress we made and the staggering amount of potential I believe Category Theory has in the field of Deep Learning.

Deep Learning is notoriously an ad-hoc field. Despite its tremendous success, we lack a unifying perspective for this growing body of work. We have entire paradigms of how to effectively learn, but it’s still hard to precisely state what a neural network is and cover all the use cases. This is the contribution of our paper. We’re making a step forward in that regard by creating a foundation of neural networks terms of three things: 1) Parameterized maps, 2) Bidirectional data structures (Lenses/Optics) and 3) Reverse derivative categories.

Since our work is based on category theory, you might wonder the aforementioned concepts are, what Category theory even is, or even why you would want to abstract away some details in neural networks? This is a question that deserves a proper answer. For now I’ll just say that our paper really answers the following question in a very precise way: “What is the minimal structure, in some suitable sense, that you need to have to perform learning?”. This is certainly valuable. Why? If you try answering that question you might discover, just as we did, that this structure ends up encapsulated some strange types of learning, with hints to even meta-learning. For instance, after defining our framework on neural networks on Euclidean spaces we realized that it includes learning not just in Euclidean spaces, but also on Boolean circuits. This is pretty strange, how can you “differentiate” a Boolean circuit? It turns out you can, and this falls under the same framework of Reverse derivative categories.

Another thing we discovered is that all the optimizers (standard gradient descent, momentum, Nesterov momentum, Adagrad, Adam etc.) are the same kind of structure neural networks themselves are - giving us hints that optimizers are in some sense “hardwired meta-learners”, just as Learning to Learn by Gradient Descent by Gradient Descent describes.

Of course, I still didn’t tell you what this framework is, nor did I tell you how we defined neural networks. I’ll do that briefly now. One of the main insights from our paper is that entirety of neural network learning can be framed in the language of optics, a bidirectional data structure used to encapsulate the essence of the forward-backward interaction (very closely related to lenses). This forward-backward interaction is animated below and summarized here.

Optics tell us that data is propagated forward, some intermediate state is saved, and then data is propagated backward - and nothing else¹. This is actually great, because we can then instantiate optics in a variety of settings. From propagating back gradients, to interesting things like propagating back utilities in game theory, to using optics for lawful updates - encapsulating the previously mentioned optimizers. But the general idea of optics is - just pick a base space/category/setting in which you can compose processes in sequence and in parallel - and then you can form the space/category of maps which are bidirectional.

Optics themselves can too be put in sequence and in parallel, in completely natural ways you’d expect. Below you can see an animation of sequential optic composition, summarized here.

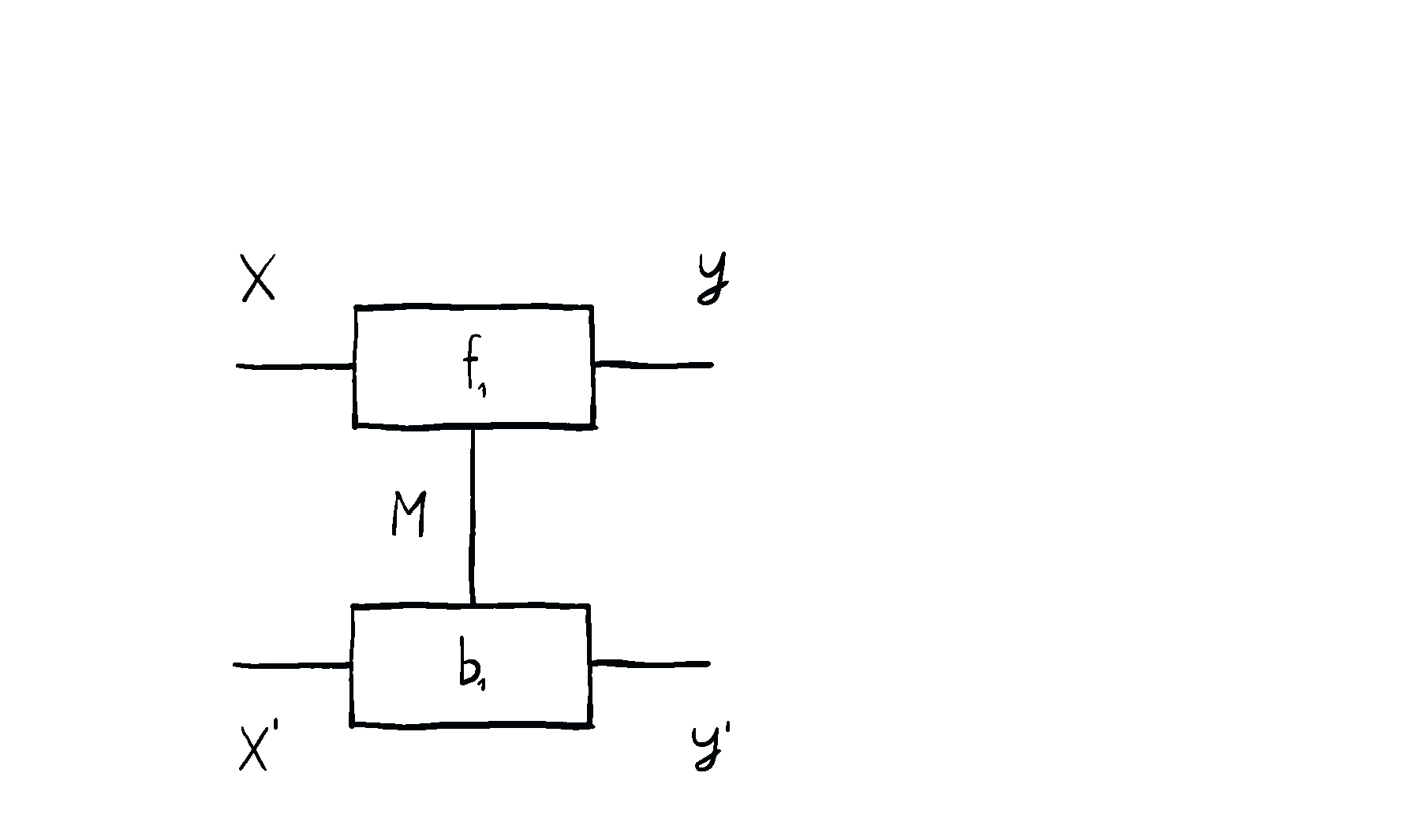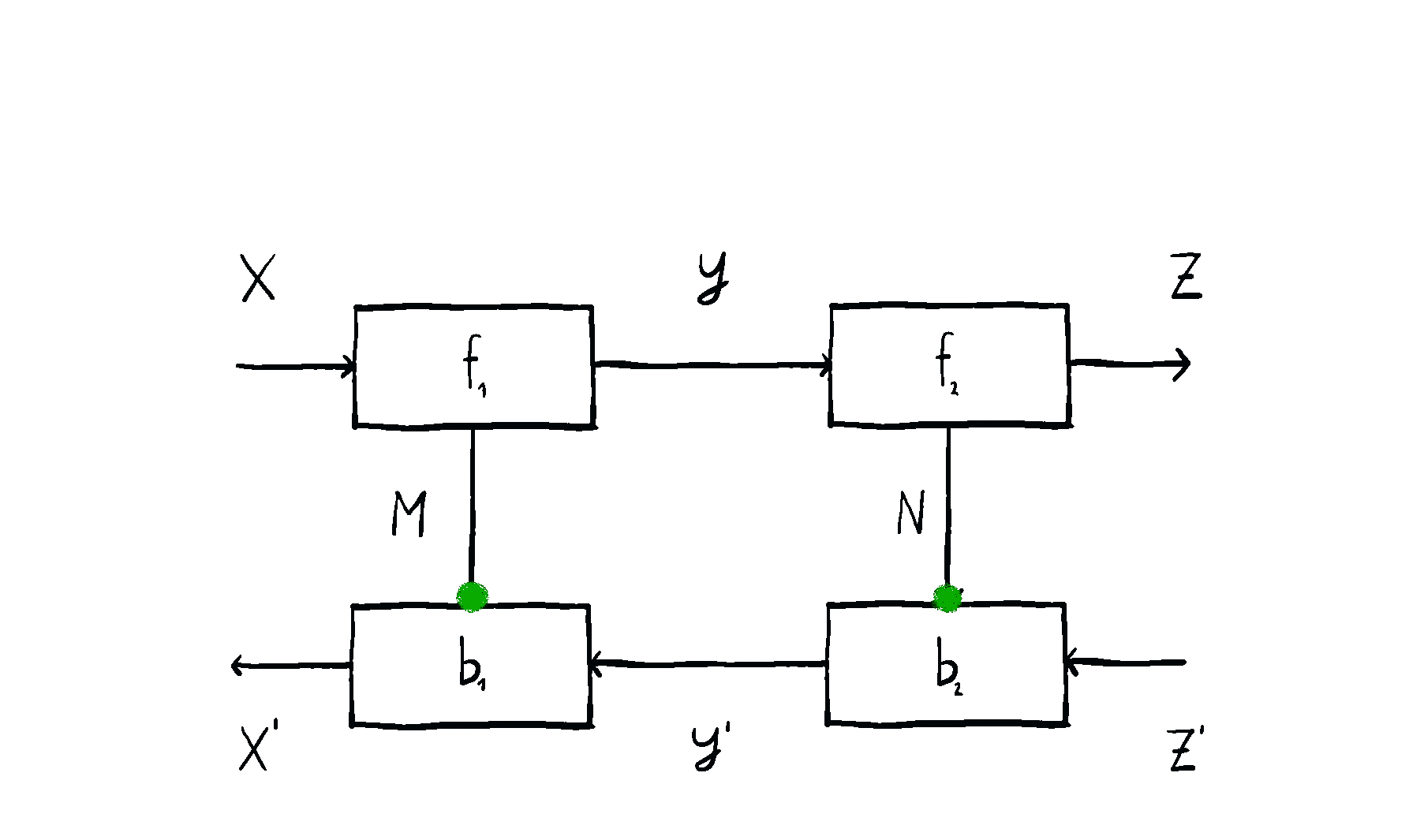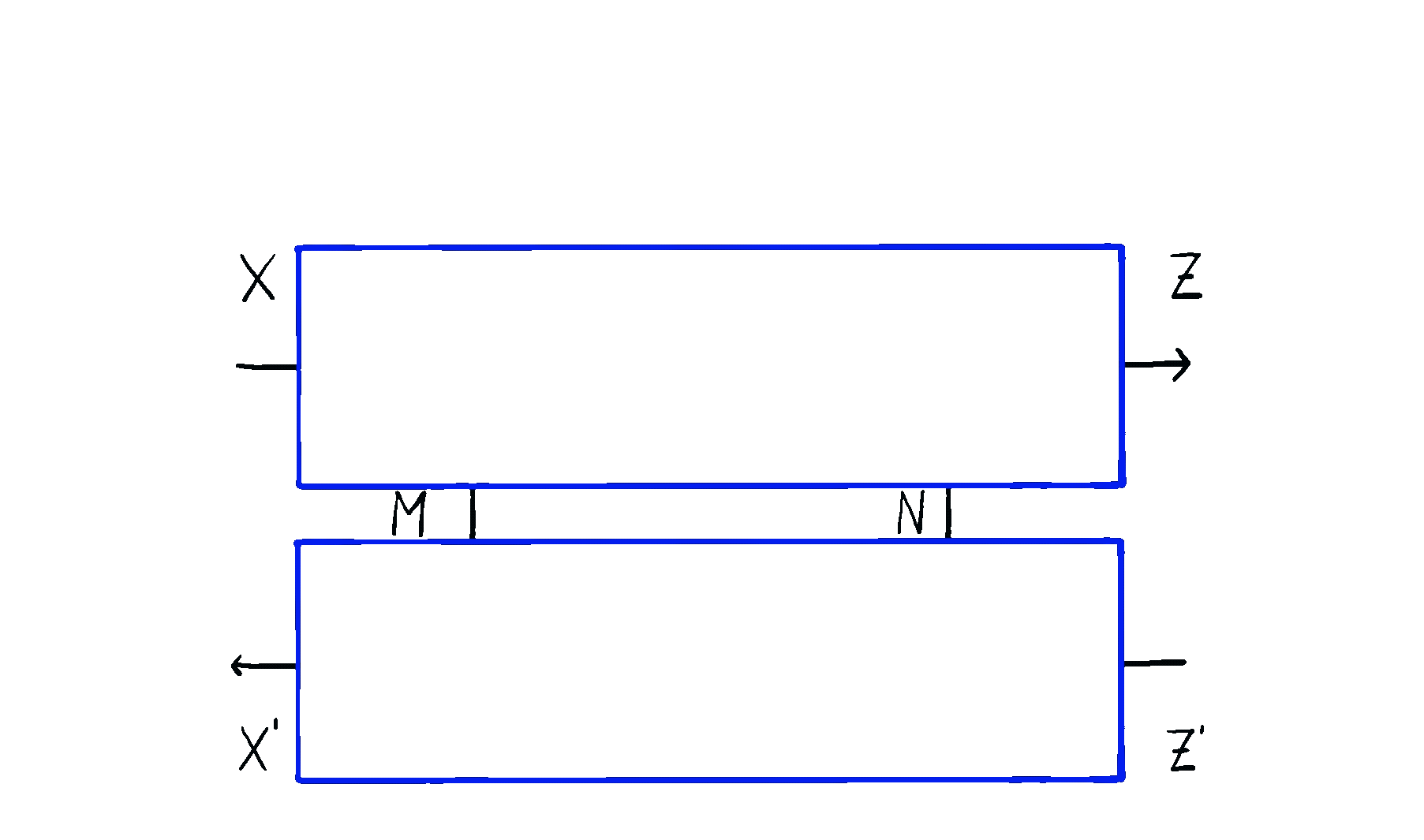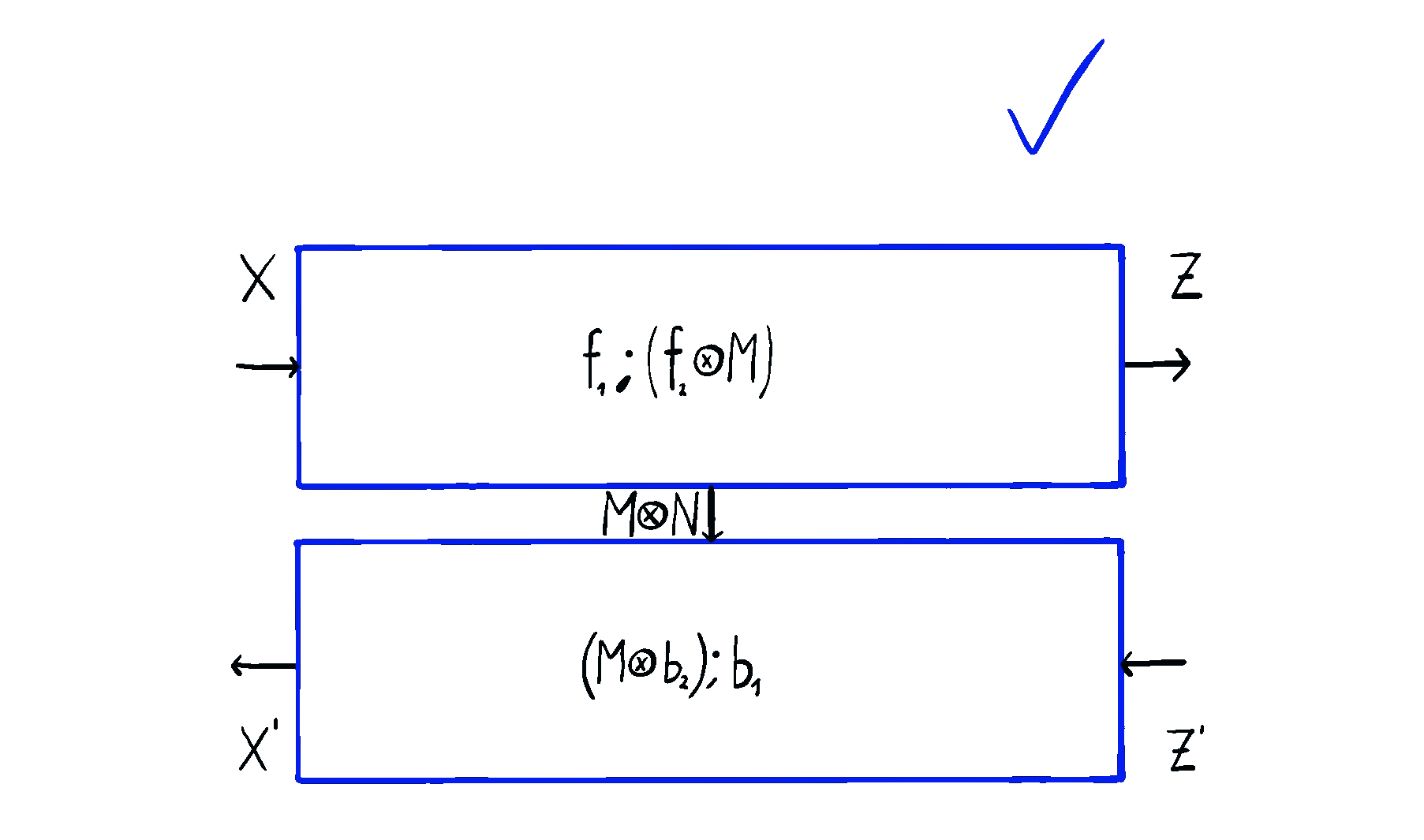
But optics by themselves aren’t enough. To talk about neural networks - or reinforcement learning agents - we need to allow optics to read from and write to some state that’s not accessible to the outside world. This is where the construction comes in. Given any base space/category/setting in which you can put compose processes in sequence and in parallel, you can form the “parameterized” space of maps which have a “hidden” input. You can think of this as the private knowledge of the agent, or as the agent’s internal space. These parameterized maps have all the nice setting you’d want - including parallel and sequential composition, as shown below.

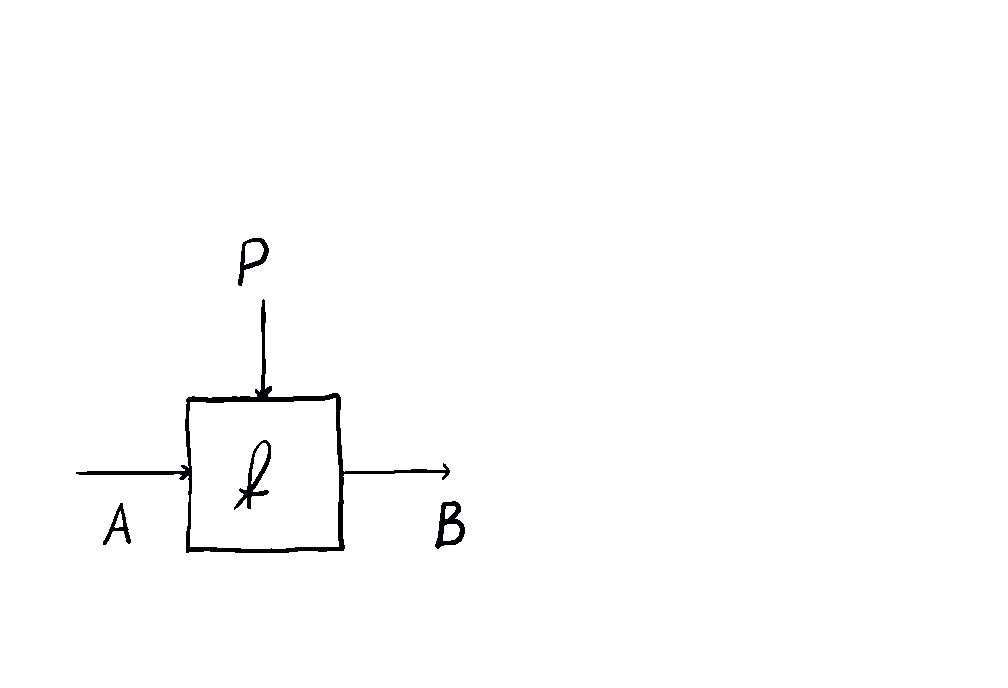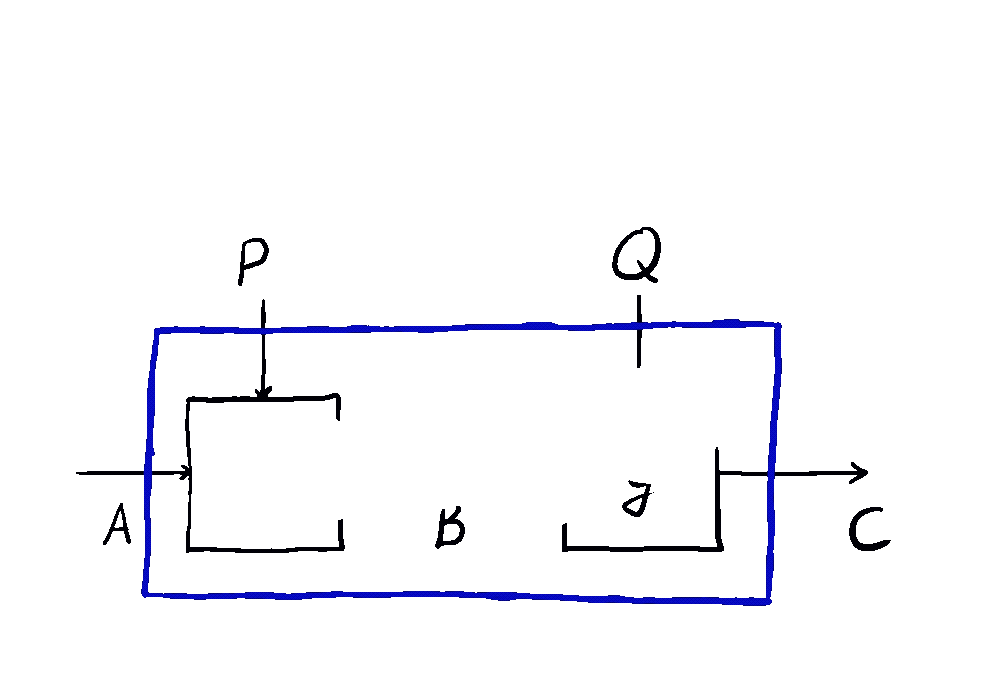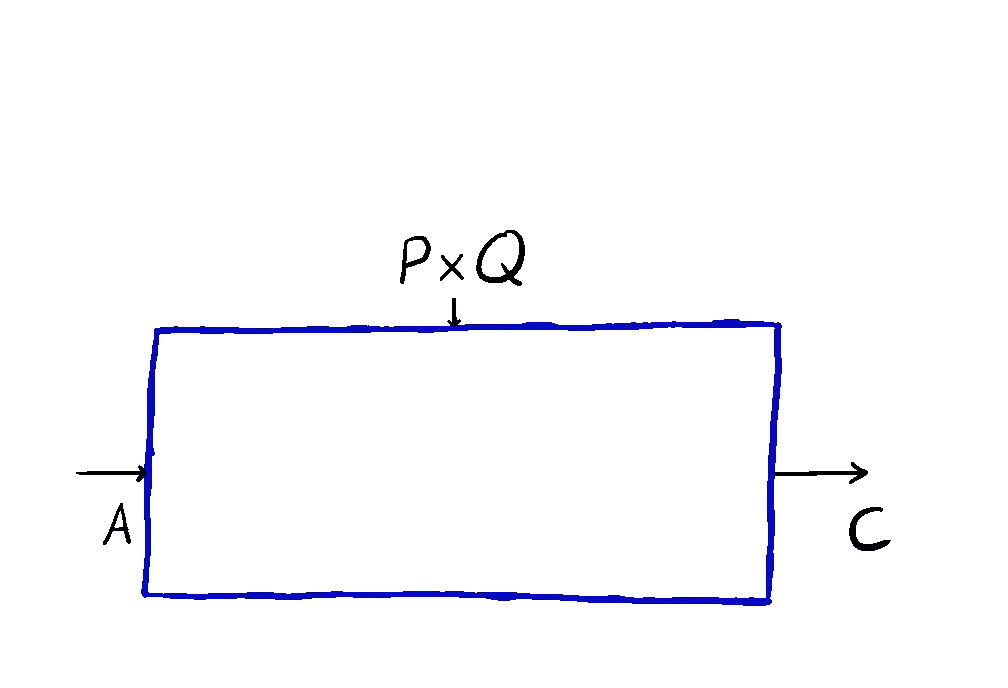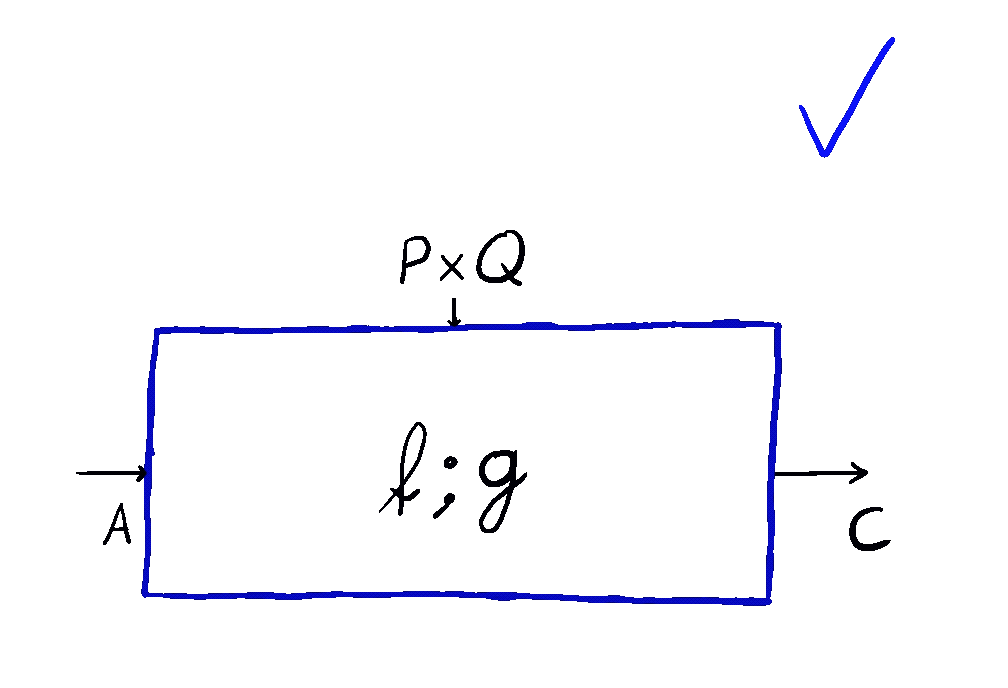
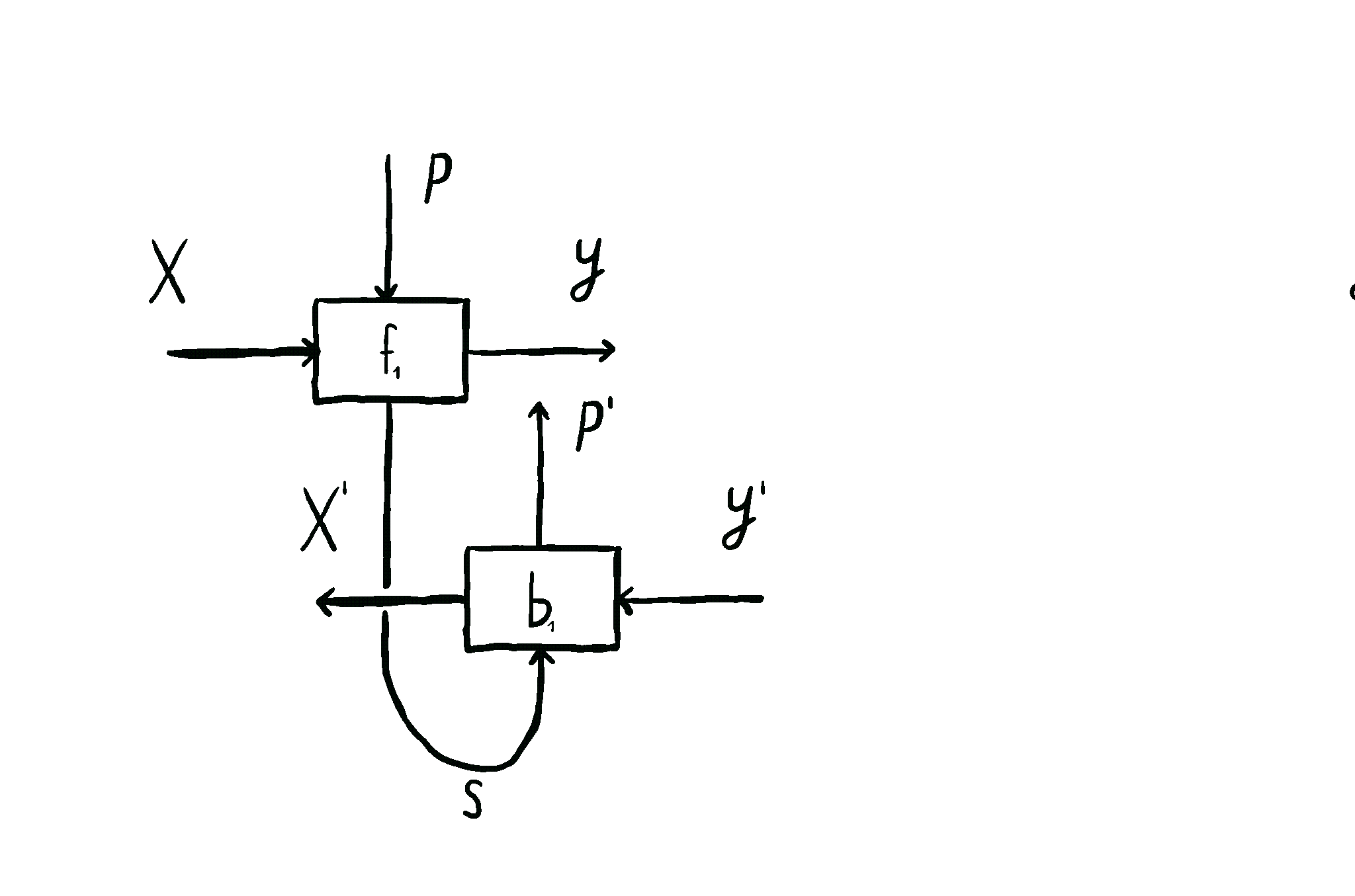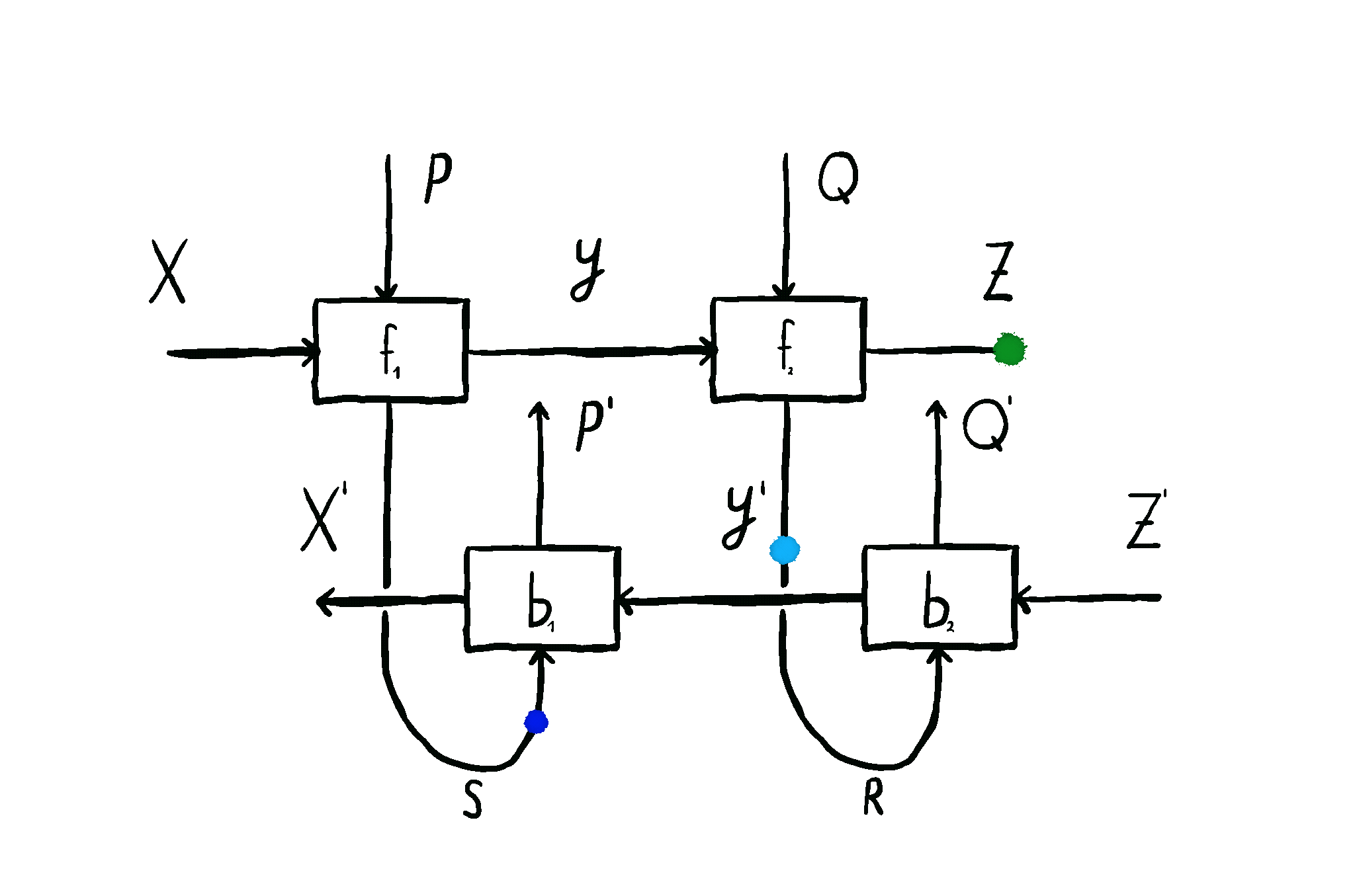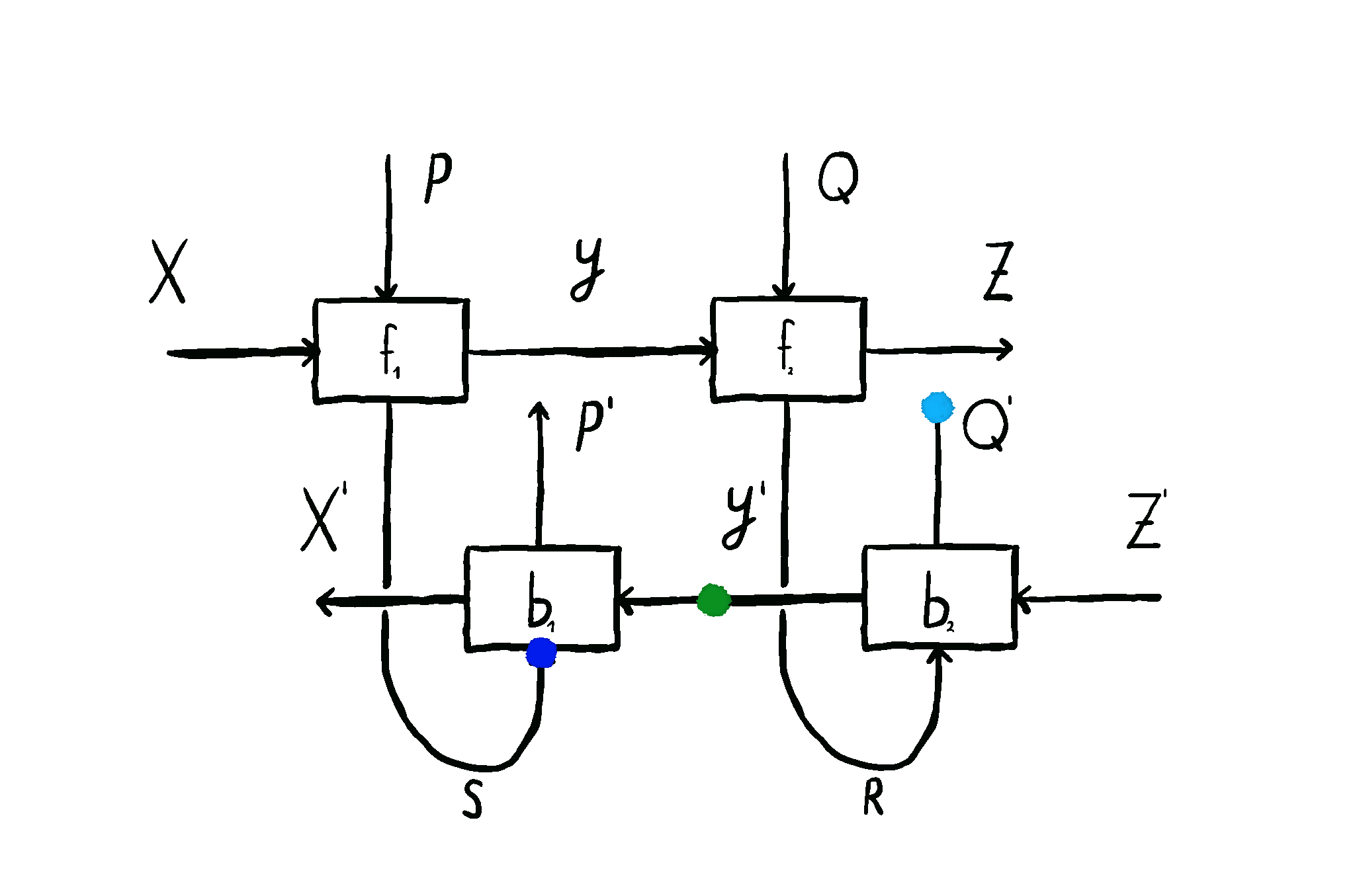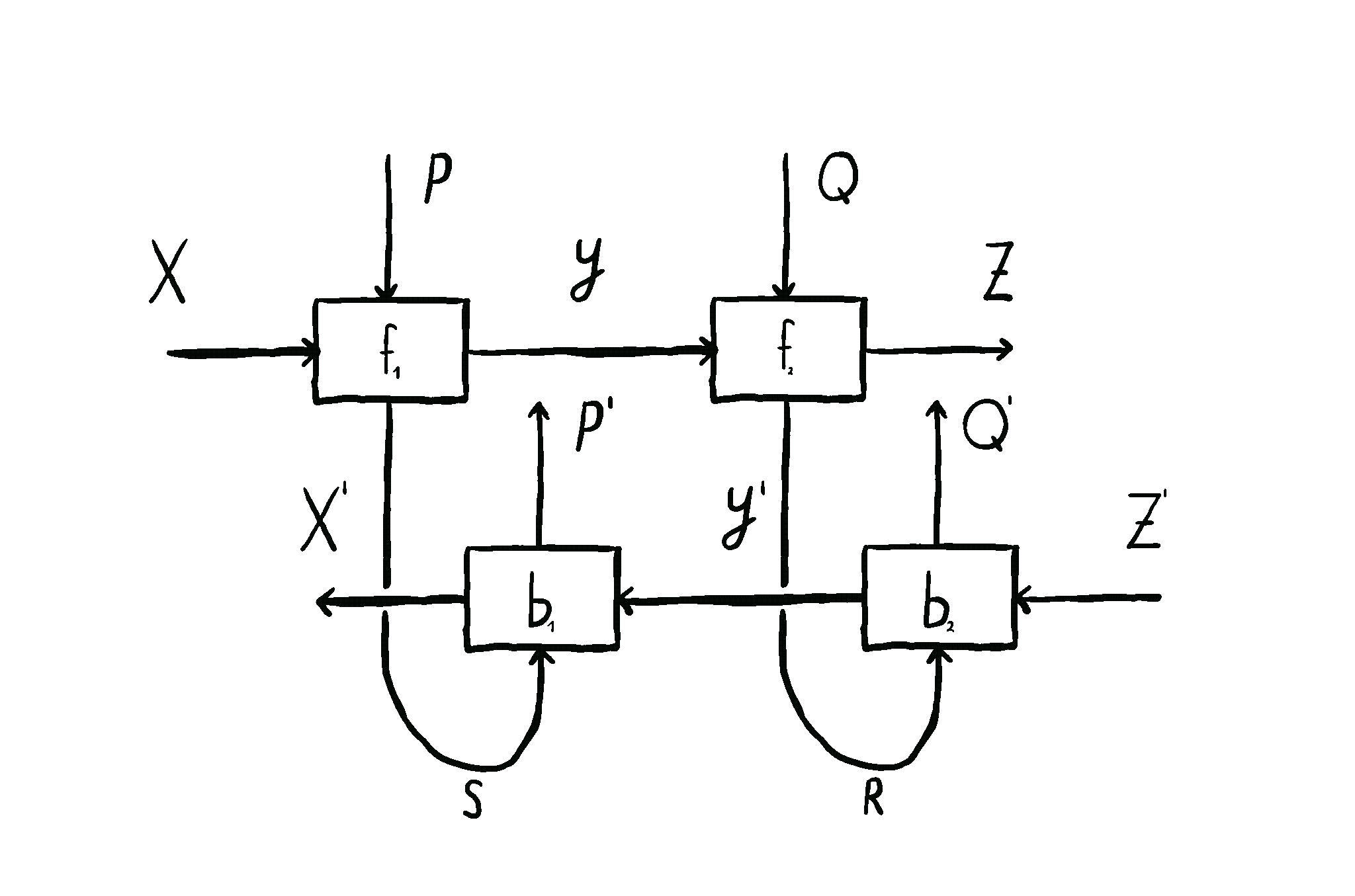
This is how we come to the main idea of our paper. by itself is not that useful, but when we apply it to , we get interesting things out. This gives us the the important notion of : the category of parameterised optics. It’s a pretty complex beast, but maps inside are in some sense the “true shape” of neural networks. A parameterised optic is here a thing with 6 ports in total, organized in (input,output) pairs on its left, right and “internal” (drawn on the top) side. It has a pretty complex flow of information, being bidirectional, but “in one additional dimension”.

The image below shows this information flow, which is also explained in more detail here, and here.

These parameterised optics can be plugged in in sequence, in parallel, and it even turns out they form something called a topos - allowing us to talk about the “internal language” of a learner, a deeply exciting prospect. They model not just neural networks, but agents found in game theory as well. And as mentioned before, these optimizers which update the parameters of these learners are exactly of the shape of these learners themselves - opening up interesting questions about meta-learning.

There are all these various things you can do with them - and this is where the power of this framework comes in. But I’ll describe these things in future posts.

This short blog post was a fast, bumpy tour of a lot of the things that we’ve been working on here at MSP. For a slower and more nuanced description check out our paper, or some of the many interesting related papers I collect in this github repository.

There is so much more to do in this setting. The deep learning community is exploring a number of exciting neural network paradigms and ideas. From Generative Adversarial Networks and Transformers, over Graph Neural Networks to very strange ideas such as World Models and Differentiable Neural Computers. Understanding their categorical essence is part of our future work and I urge anybody with overlapping interests to get in touch.